Task: Use F(x) = pi x^2. Evaluate F for x=-2:.1:2; Use gradient to estimate the first derivative. Plot the estimated derivative and the analytical derivative on a single plot. Calculate the integral of F from -2 to 2 using trapz. Compare the estimated answer to the analytical answer.
It is often necessary to estimate derivatives and integrals of quantities given a list of values. Often we don't know the true underlying function so there is no way to use the tools of calculus to analytically calculate integrals and derivatives.
There are a variety of issues associated with numerically estimating integrals and derivatives from a set of numerical values. We will avoid this discussion and just consider the simplest case where we have a list of values of some function at evenly spaced intervals.
A derivative is an estimate of a difference (or a slope of a line). The MATLAB function dF=diff(F); calculates the difference between successive values in a list. This would seem to do most of the work in estimating the derivative. Given the distance between the values in the list (dx), then the derivative is dFdx=diff(F)/dx;. For closely spaced values, this is a good estimate.
However, there is a small issue; diff returns one fewer value than the original list. Think about it. If there are three values in the list, then diff will create only two differences: the second minus the first and the third minus the second. So, dFdx=diff(F)/dx; estimates the derivative in the center of the interval between the input values. This is ok, but it can create various problems.
There is another MATLAB function (dF=gradient(F);) which estimates the derivative but returns the same number of values as the input list. It also assumes constant spacing between the values of F, given by dx, so the derivative is dFdx=gradient(F)/dx;.
Gradient is designed to calculate the derivative of a 2D function if you pass it a table of values. Since we are passing only a list (a 1D function), it calculates the simple derivative (or difference).
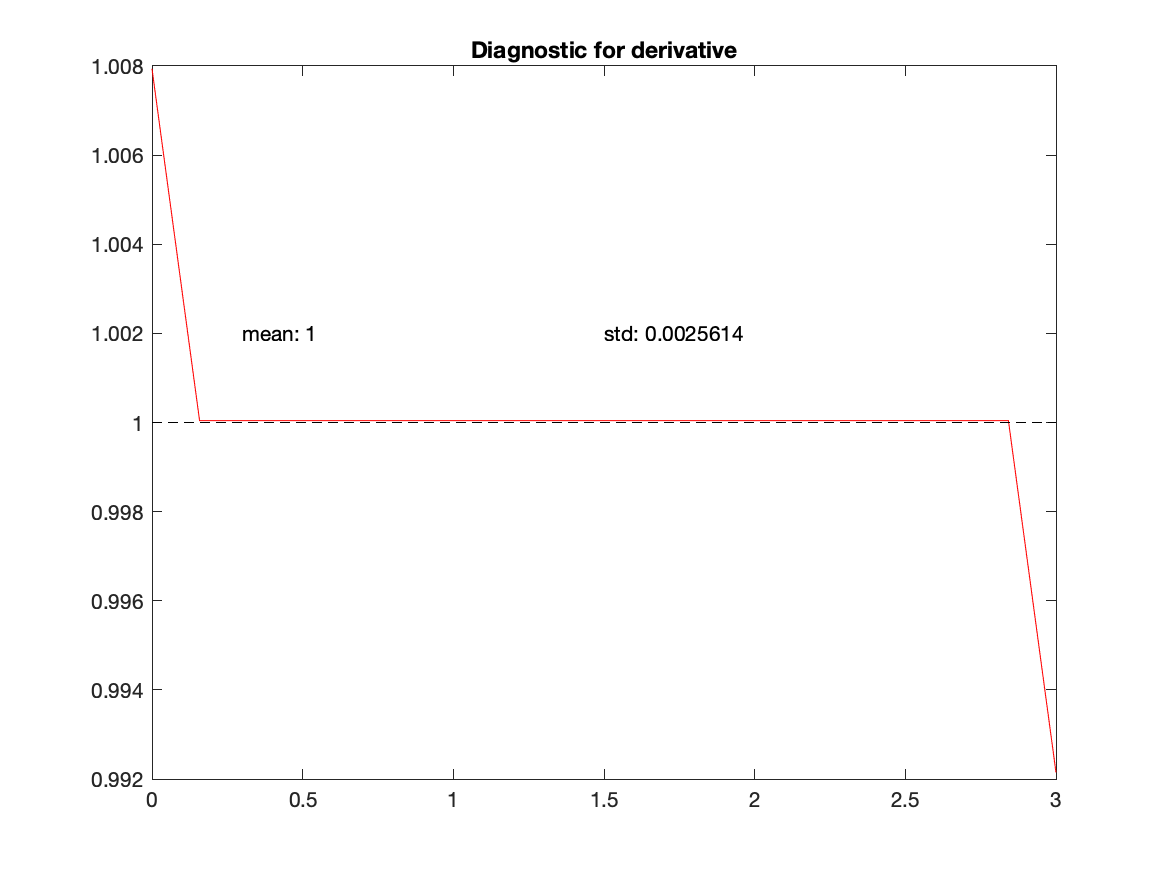
We can illustrate these ideas with a simple example. We use another MATLAB function (linspace) which creates an evenly spaced list of numbers between two limits. So, let x = linspace(0,3,20); which created 20 values evenly spaced between 0 and 3. We use this in the following example:
x=linspace(0,3,20);
F=exp(.1*x);
truedFdx=.1*exp(.1*x);
dx=x(2)-x(1);
dFdx=gradient(F)/dx;
Test=dFdx./truedFdx); % all values should be 1.0
mT=mean(Test);sT=std(Test); % see quality of answer
figure
plot(x,Test,'r',x,ones(size(x)),'k--')
title('Diagnostic for derivative')
By increasing the number of values used in linspace, the
estimated derivative
will be increasingly close to the true derivative (try it).

The opposite operation is the integral. This is basically a sum of the values, or the area under the curve. Again, there are details associated with the implimentation of a numerical integral, but we will consider the simple case of the integral of a set of uniformly spaced points.
The function s=cumsum(x); makes a cumulative sum of values in a list. So,s(1) = x(1), s(2) = x(1) + x(2), s(3) = x(1) + x(2) + x(3), and so forth. The last value of s is the sum of all values of x. This function would seem to be a way to estimate the integral from a list, which is almost true.
The function to use for an integral is trapz, which uses the composite trapezoidal rule to estimate the area. For each pair of points, a trapezoid is constructed by connecting the two points and extending a line from the points to the x axis forming a trapezoid. The area of the trapezoid is the average of the two sides times the distance between the two sides. Do this for each pair of points and add them. A test case is
x=linspace(0,3,20); F=exp(.1*x); dx=x(2)-x(1); Int=trapz(F)*dx; True=(exp(.1*3)-1)/.1; disp(['Fractional error is ' num2str((Int-True)/True)])
Finally, if you know the function that you want to integrate, there is a "functional integration" routine: INT=integral(@FUN,0,3), where FUN(x) is a MATLAB function (in a file called FUN.m). You could create the following file:
function F=FUN(x) % Function to integrate F=exp(.1*x);and test this answer against the one you got above with trapz.
Flow chart for answer %%% create x, evaluate F %%% calculate the analytical derivative %%% plot the extimated and analytical derivatives %%% compare answers %%% calculate the analytical integral %%% calculate the estimated integral %%% compare answers
Solution script for task:
%%% create x, evaluate F
%%% calculate the analytical derivative
n=2;
x=-2:.1:2;F=pi*x.^n;aFP=n*pi*x.^(n-1);
nFP=gradient(F)/.1;
figure
plot(x,F)
title('Function')
%%% plot the extimated and analytical derivatives
%%% compare answers
figure
plot(x,aFP,'k-',x,nFP,'r--')
title('Derivative of function')
%%% calculate the estimated integral
nIF=trapz(F)*.1;
%%% calculate the analytical integral
aIF=(pi/(n+1))*(2^(n+1) - (-2).^(n+1));
%%% compare answers
disp(['Integral of F is ' num2str(aIF) ' ' num2str(nIF)])